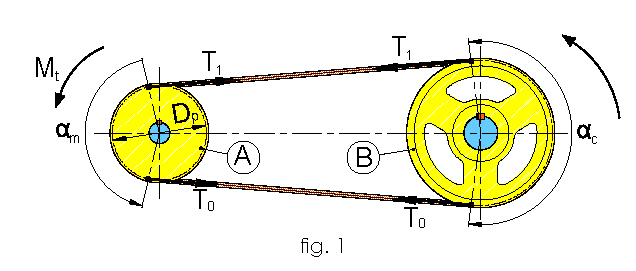
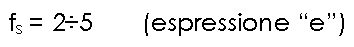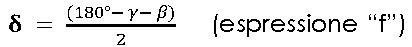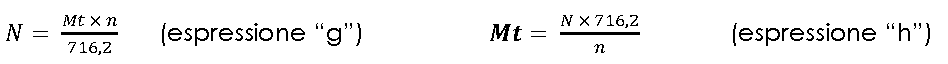Belt transmissions usually consist of a closed ring belt and two pulleys, one of which is driving and the other driven. There are various types of belts on the market, but the most utilized are: flat belts, round belts and Poly-V belts but mostly V-belts in their different sections: Z-A-B-C-D-E etc. When it comes to toothed belts you need to consult the dedicated chapters because they are positive drive transmissions. Even if there are different kinds of belts they all follow one general operating principle that determines the base rules of the design, calculations and execution of the transmission fig. 1
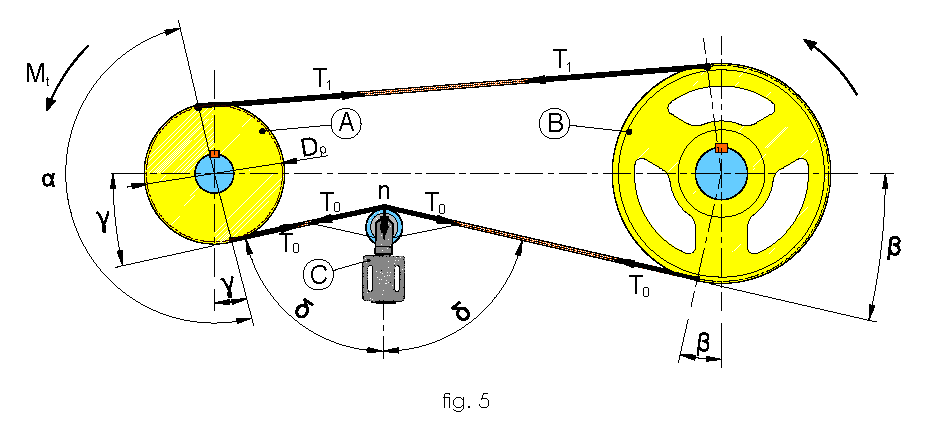
- A = Driving pulley
- B = Driven pulley
- C = Belt tensioner
- Dp = Pitch diameter of the driving pulley
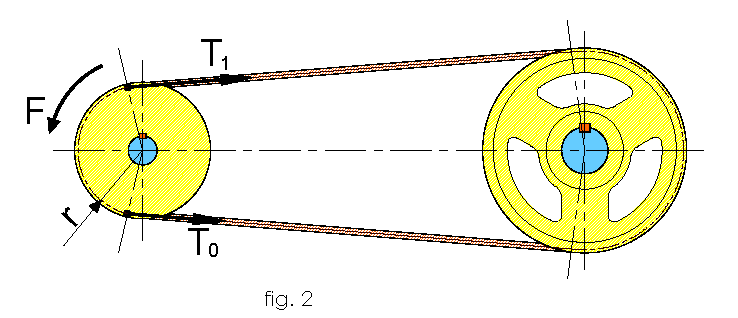
- F = Driving force
- T1 = Tension on the tense branch
- T0 = Tension on driven branch
- Mt = Momentum on drive shaft
- r = Radius
- αm = Winding angleonf driving pulley
- αc = Winding angle on driven pulley
Ideal application conditions are given by:
Correct development of the belt’s tension Full contact of the belt on the pulleys in correspondence of the winding angles am and ac With these premises in mind it is evident that the ideal condition to allow the proper functioning has to satisfy the expressions:
F ≤T_1 (expression a) and T1=T0 (expression b) fig. 2
Unfortunately real working conditions have some issues, First of all, you can’t always grant the transmission ratio because of errors or inconveniences such as:
- Wrong belt development
- Low winding angles αm (driving pulley) and αc (driven pulley)
- Low friction coefficient “η” for direct or derived causes
- Vibrations or intermittent funcitoning
- Inadequate belt tensioning
Each and every of these above mentioned anomalies can cause the belt’s slippage out of the pulleys and functioning errors, such as speed variations and the reduction of the transmitted torque. To eliminate all of these problems you need to use an automatic belt tensioner that recovers the belt’s stretching, absorbs vibrations, increases the winding angles but most importantly it grants the belt’s tension; its use creates a node “n” in the contact point of the tensioner roller with the belt and it’s in this position that the forces at stake emerge and produce the results T0 and T1 that determine the minimal equilibrium condition for the production of motion. (fig. 3).
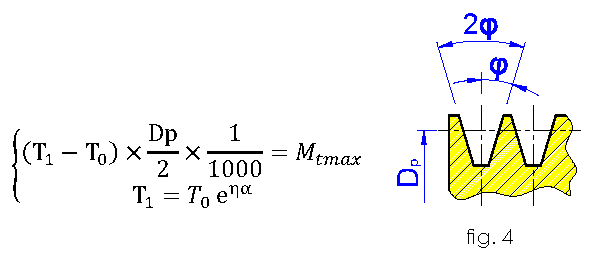
The belt tensioner has to be chosen based on the pull on the two shafts of the belt, “T1” and T0”; their value is calculated by writing the equations for equilibrium and limit of the transmission, which are “equilibrium equation at the rotation of the driving pulley” (expression “c”), together with “limit condition to sliding” (equation “d”); since the winding angle αm on the driving pulley is lower than αc and it has to be at least 180° that corresponds to πrad; the system that calculates the pulls T1 and T0 is:
e = Nepero’s number, costant equal to 2,72
ɳ = Friction ratio between the belt and the pulley
Mt = Momentum that has to be transmitted
Mtmax = Momentum on the drive shaft
fs = Service factor from 2 to 5
As it is known, all machines have critical points, such as the starting moment or their peaks of work for which you need to multiply the torque that has to be transmitted “Mt” (see next expression “h”) by the service factor “fs” to obtain the maximum work torque “Mtmax” = fs x Mt (see next expression “d”)
The belt tensioner has to be installed on the slow shaft, the closest possible to the driving pulley and it has to develop enough force to equilibrate the result of the sum of the two components of the slow shaft’s transmission. For the correct functioning of the tensioner you have to respect the indications on page 15-16 for axial tensioners and on page 19-20 for rotational tensioners.
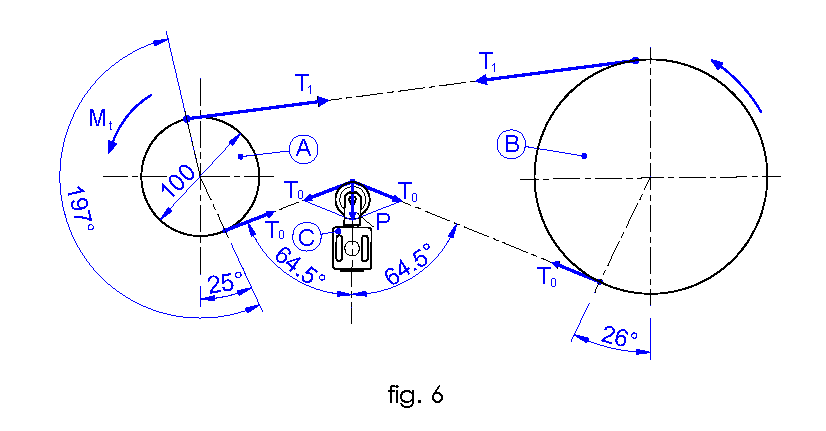
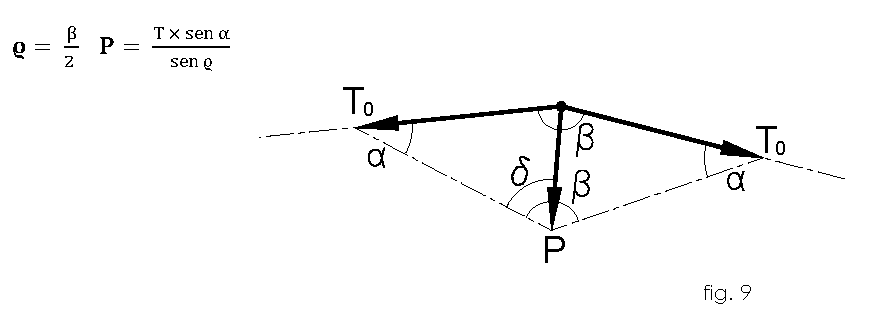
For their proper functioning it’s fundamental for it to be positioned in a way that the angles “δ” both of entry and of exit in the node “n” are equal (fig.5). Picture 5 shows the correct assembly of the tensioner on the slow shaft of the transmission;
The configuration is such to form an exit angle of the belt from the driving pulley of γ degrees compared with the vertical, while on the driven pulley of β degrees compared to the vertical; this makes it so that the angles "δ" of work are equal and result:
The conditions we just described are the minimal equilibrium conditions for the proper functioning of the belt; we present you in the following a calculation example.
Given the force value P, we can choose the tensioner, it has to be able to develop a 30% higher maximum force, It can in this way be installed on the machine within a range where the force P only requires 2/3 of its push to obtain enough pressure to grant the motion transmission in a condition of established equilibrium. Up to this point we only took into account belt transmissions working in ideal conditions and considering the highest level of functioning, which is the “equilibrium” condition; but the reality is well different and working conditions continuously change based on external factors that intervene, we only quote the most common ones:
- Starts
- Stops
- Peaks of load
- Speed variations
- Overcharges
- Errors in the development of the belt
- Environmental conditions
- Operating temperature variations
- Work cycles
- Pulley’s wear
- Belt’s wear
- Conditions and wear factors
- Specific issues
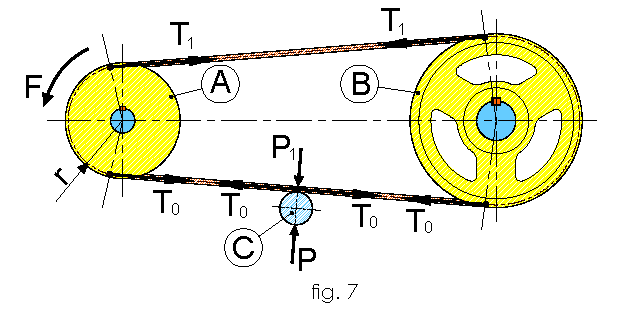
Each and every of these incidences modifies the geometry and the state of the transmission, in order to increase the reliability of the machines you need to intervene beforehand to prevent eventual issues. Representing a typical belt transmission, fig.7, we can see that the motion is granted in the moment in which the equations of the transmission are correct; in which force “N” (expression “g”) and the transmitted torque “Mt” (expression “h” ) do not depend on the number of rounds “n”:
- A = Driving pulley
- B = Driven pulley
- C = Belt tensioner
- r = radius = b (arm)
- T1 = tension on the driving shaft
- T0 = tension on the driven shaft
- F= driving force
- Mt = momento sull’albero motore
- P = force produced by the belt tensioner
- P1 = reaction
Torque Mt is calculated: Mt = F x b (expression “i”) For which F = Mt/b (expression “l”)
From these expressions we deduce that the equilibrium condition is represented by F ≤T_1 since T1=T0 F ≤T_0 (expression “m”)
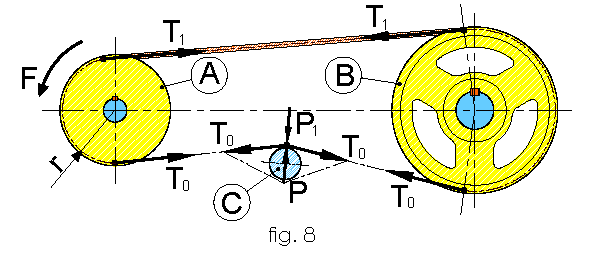
The application of the belt tensioner creates a node “n” in which the forces into play emerge; this modifies the geometry of the transmission; as a result of the force “P” developed by the belt tensioner the two trees of the belt move the node “n” up towards the equilibrium state P1 which is the reaction to P and creating the angle “β” between the two belt’s shafts; the equilibrium forces of the system have to develop on these vectors fig. 8
To determine the force of the belt tensioner to use you need to construct the parallelogram of the force’s system having i β,α and ϱ as angles emerged from the equilibrium state as an effect of the force P fig. 8. Since the force “F” is known for the equilibrium state we determine also T1 and T_0 ≥F so I can construct the graph fig. 9 and solve the following equation:
In short, a belt transmission is granted when the belt is adequately pulled and this is maintained from the dismantling of the force of the belt tensioner that based on the angle β it produces forces T corresponding at the minimum pull to grant the force F.